A Simple Neural Network from Scratch
August 29, 2025 in Machine Learning23 minutes
In this post, we’ll explore building a neural network from scratch, for whatever definition of “from scratch” includes the use of Python. This means no third-party libraries like PyTorch, Tensorflow, even Numpy.
Follow to the end for an interactive notebook which contains the full working code!
There are many types of neural networks, but in particular we’ll be building a feed-forward, multi-perceptron network. This sounds fancy but it will actually be one of the more straightforward types to build, especially in this manner.
The Problem
A classic input set to use when starting in on deep learning is an XOR table (x1 and x2 are inputs, y is the “target” - in other words, the “correct” answer):
| x1 | x2 | y |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
This problem is nice because we can wrap our heads around it quite easily, and can also get it to predict the right answer with a simple network topology. It’s also nonlinear (as you go through the inputs list, y goes from 0 to 1 but back to 0) so it’s more obvious if we haven’t gotten things quite right. It’s known as a binary classification task in this context (neural networks can be used for a lot of different things, but this is what we’ll be training it to solve).
Obviously we don’t need a neural network to give us the answers here - but it’s a nice, well-understood and well-bounded problem space with limited complexity so we can really focus on what our network is doing.
The Neuron
A neuron (in this context) really just boils down to a mathematical function. Okay, more like two functions, one nested in the other.
First, it performs a type of linear transformation known as a weighted sum. It takes in a set of inputs, and performs a weighted sum of these plus some bias value. If we have an input vector $x$ = [$x1$, $x2$], and one hidden neuron with weights $w$ = [$w1$, $w2$] and bias $b$, the neuron’s output is:
$$ h = x_1 w_1 + x_2 w_2 + b $$We call $h$ in this context this the pre-activation.
We then pass this value into an activation function, which “squishes” the pre-activation into a range that’s more useful for the next neuron in the chain. There are a few approaches here, but a common one (and one that we’ll use here) is the sigmoid (logistic) function:
$$ \sigma(h) = \frac{1}{1 + e^{-h}} $$The result is called that neuron’s activation, and this value is then used as an input to the next layer.
We can easily define a function which gives us the sigmoid implementation in Python:
Next, it’s time to implement our neuron by combining the activation function sigmoid() with the weighted sum.
The parameters above for the function neuron() are specific to the example provided above - we have two inputs [$x1$, $x2$], weights $w$ = [$w1$, $w2$] and bias $b$. These are specific not only to this example, but the topology of the network we’ll be setting up in the next section. Other topologies (outside the scope of this exercise) may require a different implementation.
Defining The Network
We have the neuron definition, now we need to use it in a network. For that we first need to talk about the topology of the network which will enable us to predict the correct XOR table outputs. Just about the smallest, simplest topology we can have that can be trained to reliably predict even this simple task is the 2-2-1 topology: two inputs, two hidden neurons, and one output neuron.
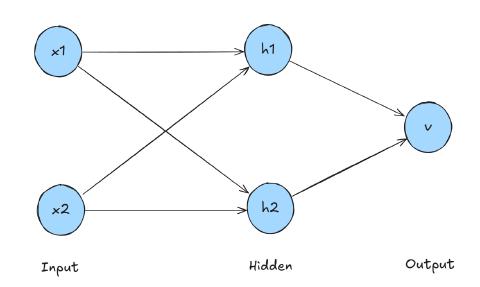
The hidden neurons follow the pattern we discussed in the previous section:
$$ h_1 = \sigma(x_1 w_{11} + x_2 w_{21} + b_1) $$$$ h_2 = \sigma(x_1 w_{12} + x_2 w_{22} + b_2) $$Our single output neuron also follows this pattern, but with some new variable names we haven’t talked about yet.
$$ \hat{y} = \sigma(h_1 v_1 + h_2 v_2 + c) $$$h_1$ and $h_2$ are the activation values from the hidden neurons, which are now serving as input to the output layer/neuron. There’s also weights $v_1$ and $v_2$ and bias $c$ which are specific to this output layer.
We’ll also be seeing some notation for each individual weight that helps us keep track of which edge it applies to:
- $w_{11}$: weight from input $x_{1}$ to hidden neuron $h_{1}$
- $w_{21}$ weight from input $x_{2}$ to hidden neuron $h_{1}$
- $w_{12}$: weight from input $x_{1}$ to hidden neuron $h_{2}$
- $w_{22}$ weight from input $x_{2}$ to hidden neuron $h_{2}$
The output from this network is $\hat{y}$ (or y_hat as we’ll refer to it in Python). Again this is from our sigmoid activation function so the value is a floating point number between 0 and 1, but this is fine because those extremes are the two possible solutions to each input. While initially this untrained network will be pretty random (though close to the midpoint of 0.5), the goal is to get the output of the network to be closer and closer to the “true” answer of 0 or 1.
This can be represented simply in Python since it’s a very small network - just making sure to run the hidden neurons first because we need their output to serve as inputs to the output layer.
1def network(x1, x2,
2 w11, w21, b1,
3 w12, w22, b2,
4 v1, v2, c):
5 # hidden neuron 1
6 h1 = neuron(x1, x2, w11, w21, b1)
7 # hidden neuron 2
8 h2 = neuron(x1, x2, w12, w22, b2)
9 # output neuron
10 y_hat = neuron(h1, h2, v1, v2, c)
11
12 # y_hat is our prediction, but we're also returning the
13 # hidden neuron outputs as well. These can be ignored
14 # if you just want the prediction - these are more
15 # useful when we get to training.
16 return h1, h2, y_hatRunning the un-trained network
In order to produce anything even remotely meaningful, we’ll have to pick some starting weights and biases. These are provided in the code below. Don’t worry about what these mean right now - just suffice it to say they’re definitely no where near correct enough to start making accurate predictions - only to show that our untrained network is functioning as we’d expect at this point.. We’ll dive into these a lot more when we try to properly train this network.
1# Input dataset
2xor_dataset = [ (0,0,0), (0,1,1), (1,0,1), (1,1,0) ]
3
4# Starting parameters
5w11, w21, b1 = 0.30, -0.20, 0.00
6w12, w22, b2 = -0.40, 0.10, 0.00
7v1, v2, c = 0.20, -0.30, 0.00
8
9# x1,x2 are our inputs, y is the "true" solution. We'll compare this
10# to what our network produces - y_hat
11for (x1, x2, y) in xor_dataset:
12 _, _, y_hat = network(x1, x2, w11, w21, b1, w12, w22, b2, v1, v2, c)
13 print(f"input=({x1},{x2}) target={y} y_hat={y_hat:.4f}")This gives us sensible “pre‑training” predictions (obviously still totally unreliable in terms of prediction capability, but also not saturated - pretty much right on the centerline), which is exactly what we want and expect before we dive into training these parameters.
input=(0,0) target=0 pred=0.4875
input=(0,1) target=1 pred=0.4831
input=(1,0) target=1 pred=0.4986
input=(1,1) target=0 pred=0.4943Now that we have a sense for how the network comes up with an answer, let’s see about training these parameters to nudge it in more of a “correct answer” direction.
Training Pass - Step By Step
To make this network useful, we need to train it. We do this by feeding in some input and measuring how far the network was from the right answer - then doing a bunch of operations to feed this back into the all of the network’s parameters so that we “nudge” them in the right direction.
Normally this is done with a large number of inputs, so that a bunch of nudges can result in a set of parameters that can make reliably good predictions. However, for now we’ll go into detail about the impact a single input has on training the network, so that when we get around to repeating for all inputs, we’ll know what’s happening at each iteration.
For a given input, there are three general steps that are followed for each layer of the neural network in order to train it:
- Get the error term for this layer’s outputs
- Compute the gradient of the loss wrt that layer’s weights and biases
- Update the weights for this layer using a gradient descent
These steps are followed from the output layer through the hidden layers, all the way back to the input layer. This chaining of loss gradients from the output layer back through the neural network is known as backpropagation.
To start, we first need to do a forward pass of our network - just like we did before, but, this time taking care to not only capture the output, but also the output weights for later.
1# We're going through the training process for a single output for now.
2# After we do this once we'll wrap this and everything else in the training
3# process so we can perform it on each input iteratively
4(x1, x2, y) = xor_dataset[0]
5
6# Forward pass (reuse our network)
7h1, h2, y_hat = network(x1, x2, w11, w21, b1, w12, w22, b2, v1, v2, c)Output Layer Error Term
The “error term” (represented by $\delta$) is very important because it basically represents how much a given neuron contributed to overall error of the network’s prediction. We want to fine-tune each parameter individually so it’s really important in backpropagation to understand which neuron’s are more to blame for a bad prediction and adjust accordingly.
To be a bit less colloquial, the error term is the derivative of the loss w.r.t. that neuron’s pre‑activation (in our case the weighted sum - the linear part before our sigmoid activation function). So, we first need to get that pre-activation value for our output neuron, called $z_{\text{out}}$. This should look a little familiar from our neuron implementation:
$$ z_{\text{out}} = h_1 v_1 + h_2 v_2 + c $$We know what the output should be (${y}$) but for training purposes we also want to know what the output neuron produced. Recall, we named this value y_hat, or $\hat{y}$.
Next, we need a loss function. This is a way to measure “how wrong” the network’s prediction was. There are a number of approaches we could use, but for this we’ll use mean squared error (MSE):
$$ \mathcal{L} = \tfrac{1}{2}(\hat{y} - y)^2 $$Use the right tool for the job!
MSE is actually not well-suited for classification problems like this! It’s better for other problems like regression. And when it came time to train this network, I definitely found this out the hard way, as I’m confident it is part of the cause for some of the convergence issues I saw during training.
A better loss function for classification problems like this would be cross-entropy. However, as I only discovered this after I had already put together most of this post, I’ve elected to continue to use MSE.
I did, however follow this up with a new blog post which correctly uses cross-entropy for the loss function, as well as a few other improvements. This was significantly (although not 100%) more reliable.
We have the loss of the network as a whole, but the point of the error term is to figure out how much of the blame for this loss should be assigned to a particular neuron. Again, this is the derivative of the loss w.r.t. that neuron’s pre‑activation:
$$ \delta_{\text{out}} := \frac{\partial \mathcal{L}}{\partial z_{\text{out}}} $$Reminder
$\partial$ is the notation for the partial derivative
We can’t directly calculate this because there’s a nested function in here. In order to know the loss $\partial \mathcal{L}$ we need to know the output of our activation function $\partial \hat{y}$, and in order to know $\partial \hat{y}$ we need to know our pre-activation value $z_{\text{out}}$. This dependency relationship is shown below:
$$ z_{\text{out}}⟶\hat{y}⟶\mathcal{L} $$So we need to use the chain rule:
$$ \frac{\partial \mathcal{L}}{\partial z_{\text{out}}} = \frac{\partial \mathcal{L}}{\partial \hat{y}} \cdot \frac{\partial \hat{y}}{\partial z_{\text{out}}} $$To get to the bottom of this, let’s compute each factor. First, the left side. The derivative of MSE w.r.t. $\hat{y}$ is:
$$ \frac{\partial \mathcal{L}}{\partial \hat{y}} = \hat{y} - y $$And for the right side, we need to use the sigmoid derivative identity:
$$ \sigma^{\prime}(z) = \sigma(z)\bigl(1-\sigma(z)\bigr) $$Applied here, derivative of $\hat{y}$ w.r.t $z_{\text{out}}$, that works out to:
$$ \frac{\partial \hat{y}}{\partial z_{\text{out}}} = \sigma^{\prime}(z_{\text{out}}) = \hat{y}(1-\hat{y}) $$So, per the chain rule, we can now multiply the two computed sides:
$$ \delta_{\text{out}} = \frac{\partial \mathcal{L}}{\partial z_{\text{out}}} = (\hat{y} - y)\hat{y}(1-\hat{y}) $$In Python, this looks like this:
1delta_out = (y_hat - y) * y_hat * (1 - y_hat)While the resulting Python code is quite simple, as you can see, some mathing needs to be done to be able to get to that point. And while the general process should be mostly the same, the specifics will be very different if different activation or loss functions are chosen.
Output Layer Loss Gradients
Next, we need to obtain the gradients of the loss w.r.t. the weights and bias. These gradients will be combined with the error term when it comes time to updating the weights/biases to nudge them towards being properly trained for this problem.
We have output weights $v_1$, $v_2$ and bias $c$, so that means we need to obtain these three gradients:
$$ \frac{\partial \mathcal{L}}{\partial v_1}, \quad \frac{\partial \mathcal{L}}{\partial v_2}, \quad \frac{\partial \mathcal{L}}{\partial c} $$Loss Gradient wrt ${v_1}$
Again, we can’t get at L directly so chain rule again:
$$ \frac{\partial \mathcal{L}}{\partial v_1} = \frac{\partial \mathcal{L}}{\partial z_{\text{out}}} \cdot \frac{\partial z_{\text{out}}}{\partial v_1} $$We already know that:
$$ \frac{\partial \mathcal{L}}{\partial z_{\text{out}}} = \delta_{\text{out}} $$which is represented and stored for us in Python-land as delta_out.
Next, we can actually pretty easily intuit the other side because we know that:
$$ z_{\text{out}} = h_1 v_1 + h_2 v_2 + c $$We’re taking the partial derivative so we only care about coefficients of $v_{\text{1}}$, which in this case is just $h_{\text{1}}$:
Now, putting the two sides together gives us:
$$ \frac{\partial \mathcal{L}}{\partial v_1} = h_{\text{1}} \cdot \delta_{\text{out}} $$Loss Gradient wrt ${v_2}$
We follow the exact same steps as above to obtain ${v_2}$ (make sure to use $h_{\text{2}}$):
$$ \frac{\partial \mathcal{L}}{\partial v_2} = h_{\text{2}} \cdot \delta_{\text{out}} $$Loss Gradient wrt ${c}$
This one is also pretty easy. We still need to chain rule:
$$ \frac{\partial \mathcal{L}}{\partial c} = \frac{\partial \mathcal{L}}{\partial z_{\text{out}}} \cdot \frac{\partial z_{\text{out}}}{\partial c} $$but we already have the evaluations for the left side from previous steps:
$$ \frac{\partial \mathcal{L}}{\partial z_{\text{out}}} = \delta_{\text{out}} $$The right side also becomes easy once you remember:
$$ z_{\text{out}} = h_1 v_1 + h_2 v_2 + c $$Again, this is a partial derivative, so we’re really just asking about the gradient of c wrt c which is of course, 1. So, all together now:
$$ \frac{\partial \mathcal{L}}{\partial c} = \frac{\partial \mathcal{L}}{\partial z_{\text{out}}} \cdot \frac{\partial z_{\text{out}}}{\partial c} = \delta_{\text{out}} \cdot 1 = \delta_{\text{out}} $$In order words, just delta_out.
Again, this results in some pretty simple Python, but how we got there was really important to cover.
Output Layer Gradient Descent
Now that we have our gradients for the output layer, we can update its parameters. We do this using a process known as a “gradient descent”. It’s useful to visualize this concept, considering the name seems to strongly imply a visual element (at least to me).
Imagine standing on the side of a mountain, and your goal is to get to the bottom. The gradients we just calculated are like a compass pointing in the uphill direction. So to move downhill, we can just do the opposite. However, we don’t want to do it too fast - in this contrived epic trek, we’re a giant which is able to take huge strides, and if we take too much of a step, we might miss the valley and start climbing another hill.
I’m clearly bad at this metaphor, so I’ll more than happily defer to 3blue1brown for a more comprehensive explanation:
We’ll represent some parameter with $\theta$, which would make our gradient:
$$ \frac{\partial \mathcal{L}}{\partial \theta} $$Before we subtract this from $\partial$, we need to first multiply by $η$, which is a learning rate of our choosing, but we’ll start small. This helps us control the “overstepping” problem I was describing poorly before.
So, the process for a gradient descent for a given parameter is:
$$ \theta \gets \theta - \eta \frac{\partial \mathcal{L}}{\partial \theta} $$And in Python, this is:
Hidden Layer Error Term
We’re done with the output layer! Now to repeat the process for our hidden layer. Again, the first step is to get the pre-activation value. Recall how this was defined for our two hidden neurons:
$$ h_1 = x_1 w_{11} + x_2 w_{21} + b_1 $$$$ h_2 = x_1 w_{12} + x_2 w_{22} + b_2 $$So, where the pre-activation value for our output layer was $z_{\text{out}}$, we’ll refer to the corresponding values for our hidden layer neurons as ${z_{h_1}}$ and ${z_{h_j}}$, or more generically as ${z_{h_j}}$ where $j$ is the node number so we can describe the formulas below which we will apply to each neuron.
Just keep in mind that the “prefix” $z$ means some kind of pre-activation output, and the subscript which follows indicates which neuron that produced it.
A reminder: the error term for a neuron is the derivative of the loss w.r.t. that neuron’s pre‑activation. With the output layer this meant using $z_{out}$ :
$$ \delta_{\text{out}}= \frac{\partial \mathcal{L}}{\partial z_{\text{out}}} $$But for hidden layer this is written in terms of ${\partial z_{h_j}}$ :
$$ \delta_{h_j} = \frac{\partial \mathcal{L}}{\partial z_{h_j}} $$In plain language, we’re trying to answer: how does $\mathcal{L}$ change when $z_{h_j}$ changes?
This time around, we’re a little deeper into the neural network, so we now have a few more dependencies to think about:
$$ z_{h_j}⟶h_j⟶z_{\text{out}}⟶\hat{y}⟶\mathcal{L} $$You’ll notice this is getting pretty long, because it also has to include the same dependencies we saw earlier with the output layer, plus this new hidden layer. Such a deeply nested relationship would normally result in quite the chain rule expression if we were doing it from scratch! Fortunately, we’ve already calculated the output layer portion of this change as $\delta_{out}$, or delta_out in Python-land, so we don’t need to recalculate it, and we can simply multiply it against the chain rule expression specific to the hidden layer:
You can imagine a predictable pattern emerging from this now that can hold for even deeper neural networks. As you move backwards in the network, you can re-use the error term that came before, and multiply by the two new coefficients required by the chain rule. As we progress, we add new coefficients. This is the crux of backpropagation.
However, before we can do that, we do need to differentiate the new coefficients, so let’s do that - fortunately this also follows the same pattern we did for the output layer. First, recall:
$$ z_{out} = h_1v_1+h_2v_2+c $$So again this can be eyeballed thanks to the partial derivative requirement:
$$ \frac{\partial z_{out}}{\partial h_j} = v_j $$And again, for the last coefficient, the sigmoid derivative identity means this works out to:
$$ \frac{\partial h_j}{\partial z_{h_j}} = h_j(1 - h_j) $$which makes our fully evaluated expression:
$$ \delta_{h_j} = \delta_{out} \cdot v_j \cdot h_j(1 - h_j) $$So in Python, we perform this for each hidden node, taking care to use the correct $j$ values for each, and re-using the precalculated delta_out:
Hidden Layer Loss Gradients
Fortunately this part is a little easier than the output layer. We already have the error term for this layer - $\delta_{h_j}$ . So to get the gradient of the loss w.r.t. the input weights ${\partial w_{ij}}$ (e.g. ${\partial w_{11}}$, ${\partial w_{12}}$, etc) we multiply by the corresponding input (${\partial x_{i}}$):
$$ \frac{\partial \mathcal{L}}{\partial w_{ij}} = \delta_{h_j}x_i $$The bias gradient? Easier still - as it is again multiplied by nothing.
$$ \frac{\partial \mathcal{L}}{\partial b_j} = \delta_{h_j} $$This leaves us with pretty simple Python:
Hidden Layer Gradient Descent
Nothing terribly new here! Simply repeating the same process we followed for the output layer.
That’s it! Now, if we ran another forward pass, we will get a different result.
input=(0,0) target=0 y_hat=0.4829
input=(0,1) target=1 y_hat=0.4786
input=(1,0) target=1 y_hat=0.4941
input=(1,1) target=0 y_hat=0.4898You’ll notice that this is just ever-so-slightly closer to the correct answer when compared to the totally naive first pass we performed. To get close to a reliable prediction, we’ll need to restructure things a bit and train this network a little harder.
Realistic Training Loop
Thus far we’ve gone through both the steps to define a network, perform a forward pass to get a prediction from the current parameters, and also have gone through a single training pass.
However, to get this network to make good predictions, we’re going to need to employ the techniques we discussed in the previous section and really hammer this network to make a whole bunch of “little nudges” in the right direction. The training loop will iterate over the entire input dataset - a single epoch. We’ll repeat this thousands of times until the parameters are giving us reliably correct predictions, and the math is telling us that the network has converged.
Before we get into the code, let’s go into some of the important concepts we’ll need to know in order to carry what we learned from our first single training run before into a “real” training loop like this.
Starting Parameters
In the earliest naive forward-pass, we picked some starting parameters by hand. It may have seemed arbitrary, but it wasn’t careless. And especially in a “real” training loop, these actually need to be chosen quite carefully. Selecting the right parameters can make or break your network’s ability to converge during a training loop quickly, or even at all! Let’s talk about a few of the potential problems:
- saturation - activation functions like sigmoid and tanh have a range of pre-activations that are ideal, and outside of this range, its gradient becomes closer and closer to zero. This can make it very difficult to calculate the true error term for a neuron. Sigmoid and tanh are known to have saturation problems, but others like ReLU are not.
- vanishing gradients - Remember, backpropagation is going to increase the amount of chain rule multiplication we have to do from the output to the input of the network. If each layer has small derivatives (from weights, activations, or both), the product continues to shrink as you go backwards. This can be caused by very deep networks, but it can also be caused by saturation.
- parameter symmetry - If parameters are initialized similarly/symmetrically, they can start computing the same thing, which isn’t what we want. Use non‑zero, mixed signs so the two hidden neurons can start learning different “directions”.
We can address most of these problems by randomly picking values for both weights and biases, within some guardrails. Note that while random initialization is usually a good thing, some of the specifics here are relevant to our particular problem and network:
- Weights, particularly hidden layer weights, need to be randomly chosen, on a fairly wide range. I found -2 to 2 or even -3 to 3 to be ideal. I had to play with this a bit and recommend you do the same. There’s no “magic” range but some intuition can apply here — too wide (say [−10,10]) will push sigmoids into saturation and the gradients vanish (no more compass). If it’s too narrow, we’ll be stuck in the middle (0.5)
- Biases should also be selected randomly and nonzero to try to shift the sigmoid left or right (this is after all binary classification), but in a much smaller range - for this problem I found the -0.5 - 5 range is ideal, so the network begins near the sigmoid’s steep region.
Retries
Our network will not always converge. It’s small, our parameters are initialized stochastically, and we have a combination of loss+activation functions which aren’t impervious to saturation. Some runs converge, some don’t — that’s normal.
Even if better activation or loss functions were employed here, the network itself is quite small, and can still have problems converging due to basic probability - there are only a handful of weights and biases in such a network - and the likelihood of symmetrical weights being picked on a random initialization is higher.
I’ve chosen to keep some of these less than ideal decisions in place - same topology, same loss function, same activation function, as I noticed that sometimes the network converges on the first try, but other times it doesn’t. So instead, I’ll be building in some “retry” functionality. We’ll detect if the network hasn’t converged, and perform the whole training loop over again.
The way we’ll determine if the network has converged or not is to explicitly check the loss value at each iteration, and see if it has or hasn’t reached some threshold. Through some experimentation, I’ve chosen that threshold to be 0.001
Refactoring
I’m also going to make this Python code a little more maintainable, readable, and re-usable:
- We’ll define a new class which not only stores our parameters, but also includes some helpful methods with re-usabilty in mind
- We’ll initialize with random parameters instead of static ones
- We’ll explicitly track average MSE for an epoch and then plot both this, and the number of correct predictions over time so we can visualize the network’s convergence
We will want to be able to plot the improvements to our model as we train it. This function will allow us to pass in a list of loss values as well as “correctness” results (comparing the true value to the predicted value), and plot both over the course of each training cycle.
Next, we’ll encapsulate all of our training logic:
- An epoch will repeat for all inputs in a dataset
- An outer loop will run until the network converges, or until some epoch limit is reached.
Try it out!
I’ve created an interactive notebook with all of this new code which you can check out below:
View this interactive marimo notebook below (best on desktop), or in a separate tab.
This should result in reliable (and reasonably fast) convergence time:
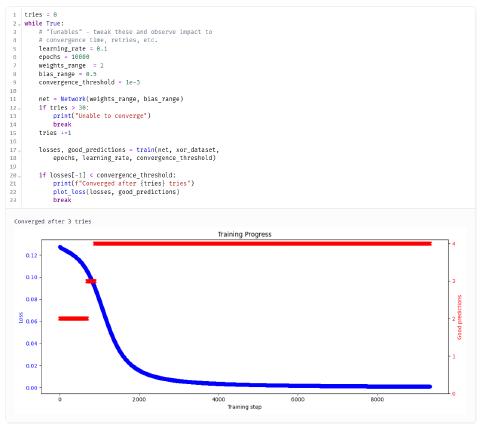
Follow-Ups
There are some loose ends I may come back to in a future post. I’d like to make some tweaks and measure their impact on convergence time / reliability. Feel free to try these yourself in the notebook above!
- I ran into slow, stalled, and even oscillatory learning during training, which led to a lot of failed convergences. This put a lot of dependence on my retry loop, where sometimes up to 20 or more retries were needed. I followed up with a new blog post that shows some significant improvements here.
- Adding more hidden neurons
- Explore other activation functions like ReLU